K Pxx R
Write the function in the form f(x)=(xk)q(x)r for the given value of k Use the remainder theorem and synthetic division to find the value of the function Factor the polynomial completely using synthetic division given one solution Verify the given factors of the function and find the remaining factors of the function.

K pxx r. The governing slenderness ratio is the larger of (KxLx/rx, KyLy/ry) KyLy/ry is larger and the governing slenderness ratio;. P(x) = n x 1;;x k px 1 1p x k k Exponential X˘exp( 1) if p X(x) = e x= , x>0 Note that exp( ) = (1 ;. Restriction of a convex function to a line f Rn → R is convex if and only if the function g R → R, g(t) = f(xtv), domg = {t xtv ∈ domf} is convex (in t) for any x ∈ domf, v ∈ Rn can check convexity of f by checking convexity of functions of one variable.
Notice that cimplies that once L(ek), k= 1,2,3, are known, the fact that Lis a linear transformation completely determines L(x) for any vector xin R3 We collect a few facts about linear transformations in the next theorem Theorem 31 Let Lbe a linear transformation from a vector space V into a vector space W Then 1 L(000) = 00. Other Bases f(x) = px, p > 0 Definition 15 For p > 0, the function f(x) = px = exlnp is called the exp function with base p Properties d dx px = px lnp ⇒ Z px dx = 1 lnp px C, for p > 0, p 6= 1 Other Bases f(x) = log p x, p > 0 Definition 16 For p > 0, the function f(x) = log p x = lnx lnp is called the log function with base p. λc = E F r K L y y y y π = 1085 λc < 15;.
(nCr button on calculator) TheBinomialTheoremprovesthat Pn x=0P(X = x) = 1whenX ∼ Binomial(n,p) P(X = x) = n x px(1− p)n−x forx = 0,1,,n, so x=0 P(X = x) = x=0 n x px(1−p)n−x p (1− p). Here we will look at solving a special class of Differential Equations called First Order Linear Differential Equations First Order They are "First Order" when there is only dy dx, not d 2 y dx 2 or d 3 y dx 3 etc Linear A first order differential equation is linear when it can be made to look like this dy dx P(x)y = Q(x) Where P(x) and Q(x) are functions of x To solve it there is a. PXZ=n(k) = P(X = k,Z = n) P(Z = n) = P(X = k)P(Y = n−k) P(Z = n) = e−λ1 · λ k 1 k!.
W x u t x g K N P J h _ N r K ` J h H r I J ~ x d J N J K e P N f ` LK f b LK f J K b I c N I b _ g ^ e W018MS0006O Submission Type Official Approval Date11/29/18 Superseded SPA ID WA SPA ID WA Initial Submission Date 9/4/18 Effective Date 8/1/18. ) Gamma X˘( ;. R x K x (LS) x C x P x Pt where A = the predicted average annual soil loss in tons per acre per year from a given slope R = the rainfall factor It is a measure of rainfall energy and intensity rather than just rainfall amount The Rfactor values for Missouri are shown in Section I(iv) K = the soil erodibility factor It.
Discover recipes, home ideas, style inspiration and other ideas to try. Let , , , , , , , ,P x y z Q x y z R x y z curl x y z P Q R = ∂ ∂ ∂ = ∇× = ∂ ∂ ∂ F i j k F F curl R Q P R Q P(F) = − − −y z z x x y, ,, ,( ) since mixed partial derivatives are equal ∇×∇ = − − − − =f f f f f f fzy yz zx xz yx xy 0 ( )( ) x y z curl grad f f x y z f f f ∂ ∂ ∂ = ∇×∇ = ∂ ∂ ∂ i j. Or we could use the fact that X is a sum of n independent Bernoulli variables.
Therefore, Fcr = ( ) 2 0658λc F y Therefore, Fcr = 2199 ksi Design column strength = φcPn = 085 (Ag Fcr) = 085 (218 in 2 x 2199 ksi) = 408 kips Design strength of column. R = Qx and K = Q then the extension F=K is not algebraic and R is not a eld 2. Background Longterm care facilities are highrisk settings for severe outcomes from outbreaks of Covid19, owing to both the advanced age and frequent chronic underlying health conditions of the residents and the movement of health care personnel among facilities in a region Methods After identification on February 28, , of a confirmed case of Covid19 in a skilled nursing facility in.
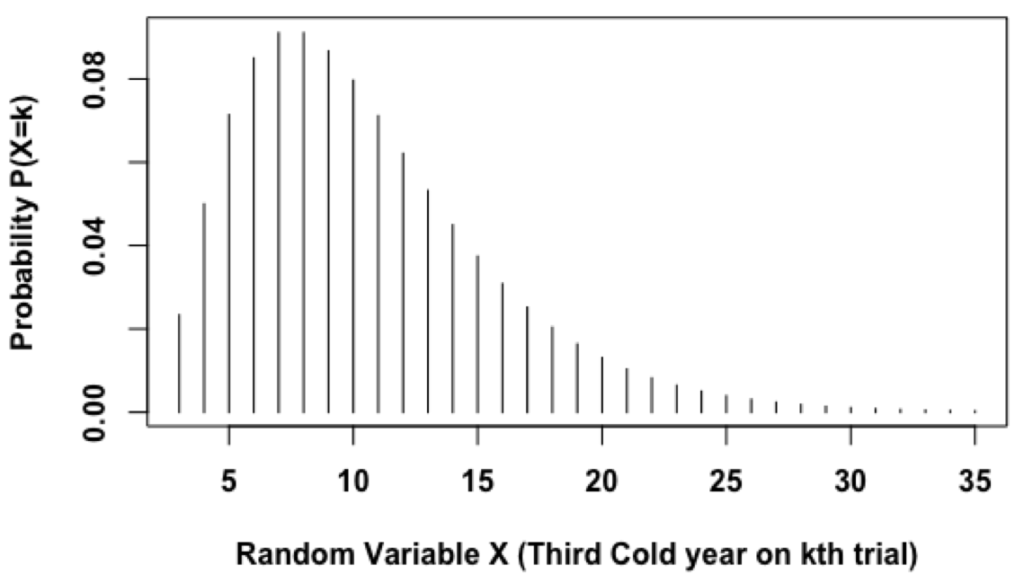
ProofLet fK g 2A be a family of convex sets, and let K = \ 2AK Then, for any x;y2 K by de nition of the intersection of a family of sets, x;y2 K for all 2 nd each of these sets is convex Hence for any 2 A;and 2 0;1;(1 )x y2 K. 325 Negative Binomial Distribution In a sequence of independent Bernoulli(p) trials, let the random variable X denote the trialat which the rth success occurs, where r is a fixed integer Then P(X = xr,p) = µ x−1 r −1 pr(1−p)x−r, x = r,r 1,, (1) and we say that X has a negative binomial(r,p) distribution The negative binomial distribution is sometimes defined in terms of the. ·e −λ2 · λ n−k 2 (n−k)!.
) if p X(x) = 1 ( ) x 1e x= for x>0 where ( ) = R 1 0 1 x 1e x= dx Remark In all of the above, make sure you understand the distinction between random variables and parameters More on the Multivariate Normal Let Y. B = f1;u;u2;;ukgfor some k Since R is a ring containing K and the basis B it follows that K(u) R As K(u) is a eld and u is nonzero it follows that u 1 is in R If the extension is not algebraic then R need not be a eld For example if F = Q(x);. Rarely used in practice Unconstrained minimization 10–7.
Title pa7pdf Author Jenniferwjakubausk Created Date 4/8/19 PM. Proof Suppose that R 6= K, and Let r 2RnK Then r 6= 0 Since r 2R F, ris algebraic over K let f K;r(x) = xn a n 1xn 1 a 1x a 0 2Kx be the minimal polynomial of rover K Since f K;r(x) is irreducible, we have a 0 6= 0 Therefore, f K;r(r) = 0 implies that r n 1 a 0 r 1 a 1 a 0 = 1 Note that a 1 0 2K R Hence, r exists. P a kxk be a power series with a nonzero radius of convergence r Then f0(x) = X a k kx k−1 for x < r Z f(x)dx = X a k k 1 xk1 C for x < r 4 Geometric series 1.
= n k · λ1 λ1 λ2 k · λ2 λ1 λ2 n−k Hence the conditional distribution of X given X Y = n is a binomial distribution with parameters n and λ1 λ1λ2 E(XX. Corresponding X value is one standard deviation below the mean If Z = 0, X = the mean, ie µ b Rules for using the standardized normal distribution It is very important to understand how the standardized normal distribution works, so we will spend some time here going over it Recall that, for a random variable X, F(x) = P(X ≤ x). K=0 n k a kb − (p(1−p))n = k=0 n k pk(1−p)n−k 1n = k=0 n k p k(1−p)n− 1 = k=0 n k p k(1−p)n− To find the mean and variance, we could either do the appropriate sums explicitly, which means using ugly tricks about the binomial formula;.
Ksuch that f(x k kp k). Induction) The following approach is often called reservoir sampling Suppose we have a sequence of items passing by one at a time We want to maintain a sample of one item with the property that it is uniformly distributed over all the items that we have seen at each step. Keeping in the spirit of (1) we denote a geometric p rv by X ∼ geom(p) Note in passing that P(X > k) = (1−p)k, k ≥ 0 Remark 13 As a variation on the geometric, if we change X to denote the number of failures before the first success, and denote this by Y, then (since the first flip might be.
Let Kbe a eld and f(X) be a separable polynomial in KX The Galois group of f(X) over Kpermutes the roots of f(X) in a splitting eld, and labeling the roots as r 1;;r n provides an embedding of the Galois group into S n We recall without proof two theorems about this embedding Theorem 11 Let f(X) 2KX be a separable polynomial of. Different texts (and even different parts of this article) adopt slightly different definitions for the negative binomial distribution They can be distinguished by whether the support starts at k = 0 or at k = r, whether p denotes the probability of a success or of a failure, and whether r represents success or failure, so identifying the specific parametrization used is crucial in any given. Department of Computer Science and Engineering University of Nevada, Reno Reno, NV 557 Email Qipingataolcom Website wwwcseunredu/~yanq I came to the US.
75 2 Binomial Theorem For anyp,q ∈ R, and integern, (pq)n = x=0 n x pxqn−x Note that n x = n!. E−(λ1λ2) · (λ1λ2) n n!. Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange.
• stopping criterion usually of the form k∇f(x)k2 ≤ ǫ • convergence result for strongly convex f, f(x(k))−p⋆ ≤ ck(f(x(0))−p⋆) c∈ (0,1) depends on m, x(0), line search type • very simple, but often very slow;. N and p, written bin(k;n;p) The probability mass function of a binomial random variable X with parameters n and p is f(k) = P(X = k) = n k pk(1 p)n k for k = 0;1;2;3;;n n k counts the number of outcomes that include exactly k successes and n k failures The Binomial Distribution. 3 WecancalculatethemeanandvarianceofY r fromthemomentgeneratingfunction, butthedifferentiationisnotquiteasmessyifweintroduceanotherrandomvariable LetX r.
Order less than or equal to kbelong to Lp ((a;b)), with the norm kfkWk;p = 0 @ Xk j=0 Zb a f(j)(x) p dx 1 A 1=p The derivatives f(j) are de ned in a weak, or distributional, sense as we explain later on More generally, if is an open subset of Rn, then Wk;p() is the set of functions whose partial derivatives of order less than or equal to. X(n')=o n40, n>(N0) Dsrt ore e'p Gorite lengfb N (or less) 0 aX(n )I YX(n)=(h) i() Ei()I no (n)(WN (X NnrN r n = on) R5Cs 1 (n' (k)=DFS of~y N o ri~n)ks~ N X (n, *nd l N X (k)= (k) = (b)R ((k)) N k 0 1, An Properi'e3, o fthe DF T Shiln Proper t(n) 1(k') o 5mme~rcqProperie S6reapi C)FS Ip (k I{)ra X. With options including phone, video, online chat and more, it’s easy to get care when and where it works for you* *If you travel out of state, virtual care may be limited due to state laws that may prevent doctors from providing care across state lines.
PX(x), satisfythe conditions a pX(x) ≥ 0 for each value within its domain b P x pX(x)=1,where the summationextends over all the values within itsdomain 15 Examples of probability mass functions 151 Example 1 Find a formula for the probability distribution of the total number of heads obtained in four tossesof a balanced coin. Suppose (a(x),p(x)) = k ·p(x), where k ∈ F and k 6= 0 Then k ·p(x) a(x), ie k ·p(x)b(x) = a(x) for some b(x) But then p(x)k ·b(x) = a(x) shows that p(x) a(x), contrary to assumption The only other possibility is that (a(x),p(x)) = k, where k ∈ F and k 6= 0 So I can find polynomials m(x), n(x), such that a(x)m(x) p(x)n(x. Jun 23, 14 · Write the function in the form f(x) = (x − k)q(x) r(x) for the given value of k Use a graphing utility to demonstrate that f(k) = r f(x) = 15x^4 10x^3 − 15x^2 11 k= 2\\3.
The rmultinom() algorithm draws binomials Xj from Bin(nj, Pj) sequentially, where n1 = N (N = size), P1 = p1 (p is prob scaled to sum 1), and for j ≥ 2, recursively, nj = N sum(k=1, , j1) Xk and Pj = pj / (1 sum(p1(j1))) Value For rmultinom(), an integer K x n matrix where each column is a random vector. Title CongregateFacilitiesGroupA_GroupB_Guidance_321xlsx Author CarrieRice Created Date 3/19/21 AM. Application of the formula using these particular values of N, k, p, and q will give the probability of getting exactly 16 heads in tosses Applying it to all values of k equal to or greater than 16 will yield the probability of getting 16 or more heads in tosses, while applying it to all values of k equal to or smaller than 16 will give the probability of getting 16 or fewer heads in.
Xk i=1 1/p (since X i ∼ geom(p)) = k/p 5 (MU 218;. Definitions and examples of Expectation for different distributions. ZTx ≤ kxk kzk∗ for all x,z ∈ Rn The dual of the ℓ p norm is the ℓ q norm, where 1/p 1/q = 1 The dual of the ℓ 2 norm on R m×n is the nuclear norm,.
K P X 1,387 likes @memeiraporamor. $=\sum_{x_k \in R_X} P_X(x_k) \int_{\infty}^{\infty} x \delta(xx_k)dx$ $=\sum_{x_k \in R_X} x_kP_X(x_k)$ $\textrm{by the 4th property in Definition 43,}$ which is the same as our original definition of expected value for discrete random variables Let us practice these concepts by looking at an example.

Multinomial Distribution Ppt Download

File Circle With Tangent Parameters H K R X Y Svg Wikimedia Commons

Elements Of Probability Lecture 3 Online Presentation
K Pxx R のギャラリー

Compound Distribution Assignment Help Statistics Homework Help

Probability And Random Process Notes

The Binomial Distribution Ppt Download

Polar Or Distance Form Of A Straight Line Equation What Is Polar Or Distance Form Of A Straight Line Equation Examples Solutions Cuemath

Sheet 3 Probability Studocu

Solved 10pts The Purpose Of This Problem Is To Show Tha Chegg Com
Lesson 40 Discrete Distributions In R Part Ii Dataanalysisclassroom

Proving That A Ring Homomorphism R X To R R P Mapsto Underline P Takes 1 To 1 Mathematics Stack Exchange

Help Maths

Expectation Calculation For Mathbb E X 2 X Le K Mathematics Stack Exchange

The Polynomial P X 2x3 Kx2 3x 5 And Q X X3 2x2 X K When Divided By X 2 Leave The Same Brainly In
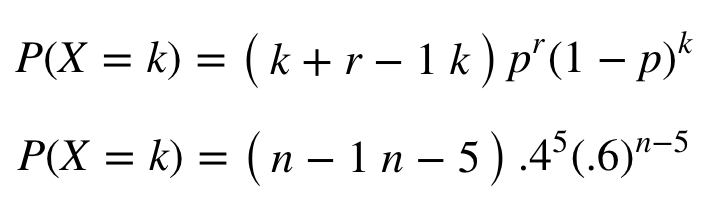
The 5 Discrete Distributions Every Data Scientist Should Know By Rahul Agarwal Towards Data Science

Use A Negative Binomial For Count Data By Ravi Charan Towards Data Science

Discrete Random Variable Questions
Journal Of Economics And International Finance Two Qualified Models Of Learning By Doing

Please Can Someone Teach Me And Help Me Solve It Probabilitytheory

Starter The Probability Distribution Of A Discrete Random Variable X Is Given By P X R 30kr For R 3 5 7 P X R 0 Otherwise What Is The Value Ppt Video Online Download

Let Sum R 1 Nsin 1 Alpha R Npi 2 For Any N In N And P

Lecture 9 5 3 Discrete Probability 5 3
Probability Mass Function Wikipedia

Solved A Bernoulli Random Variable X With Success Probabi Chegg Com

Elements Of Probability Lecture 3 Online Presentation

2 4 The Negative Binomial Distribution Is One Mod Chegg Com

Further Distributions Probability Generating Functions Ib Maths Hl

Starter The Probability Distribution Of A Discrete Random Variable X Is Given By P X R 30kr For R 3 5 7 P X R 0 Otherwise What Is The Value Ppt Video Online Download

Discrete Random Variable Questions
For What Value Of K X 1 Is A Factor Of P X Kx 2 X 4 Quora

Discrete Random Variables Ppt Download

Answer The Following And Justify I Can X 2 1 Be The Quotient On Division Of X 6 2x 3 X Youtube

Lesson 35 Trials To R Th Success The Language Of Negative Binomial Distribution Dataanalysisclassroom

14 The Cumulative Distribution Function

Answered The Discrete Random Variable X Has Bartleby
A Random Variable X Can Take All Non Negative Values And The Probability That X Take The Value R Is Sarthaks Econnect Largest Online Education Community

The Formation Of Methanol Is Important To Clutch Prep

Solved 5 The Discrete Random Variable X Has Probability Chegg Com

If The P M F Of A D R V X Is Defined By N P X 0 3 K 3 P X 1
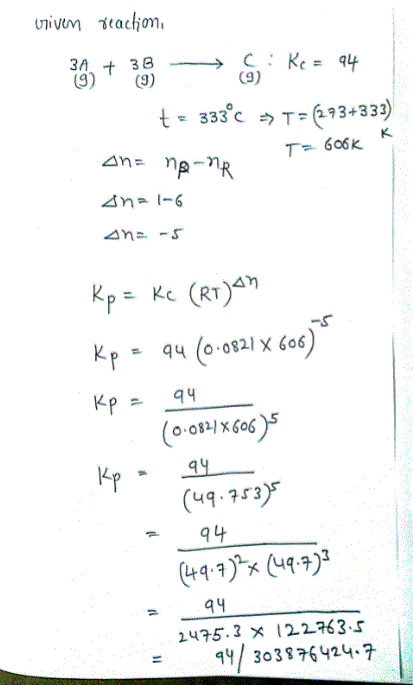
Oneclass The Equilibrium Constant Kc Is Calculated Using Molar Concentrations For Gaseous Reactio

Polynomial Ring Wikipedia

Expected Value Section 7 4 Partially Section Summary

Answered Which Of The Following Is The Power Bartleby

Chapter 3 Quantum Mechanics In Physics Ei Kr

Basic Method Of Data Mining Probability And Statistics 3 Common Distribution And Hypothesis Test

Solved 4 The Discrete Random Variable X Has Probability Chegg Com

Chapter 4 Joint And Conditional Distributions Ppt Download
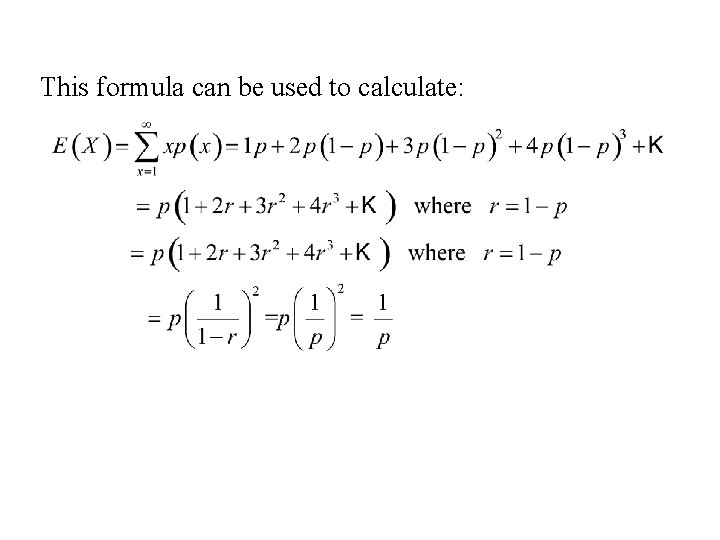
Expectation Let X Denote A Discrete Random Variable

Ta Notes Week5 Bao Zhigang Studocu
A Random Variable X Can Take All Non Negative Values And The Probability That X Take The Value R Is Sarthaks Econnect Largest Online Education Community
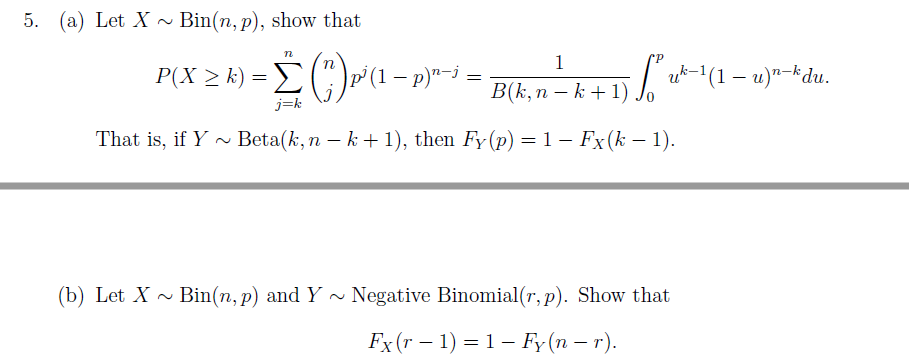
Solved 5 A Let X Bin N P Show That P X K P 1 Chegg Com

Find The Joint Distribution With 2 Discrete Random Variables Mathematics Stack Exchange

7 The P M F Of A R V X Is As Follows P X 0 3k P X 1 4k 10k P X 2 5k 1 P X

Expectation Let X Denote A Discrete Random Variable

Find The Profit Function P X Given The Cost And Revenue Function C X R X Youtube

Answered Consider The Cunc Y1 X A Find The Bartleby

7 8 Transcendency

Stochastic Modeling Of Some Natural Phenomena A Special Reference To Human Fertility Sciencedirect

Let A Random Variable X Have A Binomial Distribution With Mean 8 A

Solved For Each Of The Following Distributions Find K Su Chegg Com

View Question Suppose That X Is A Negative Binomial Random Variable With P 0 2 And K 4 Determine The Following

Putnam Training Polynomials Exercises 1 Find A Polynomial With Integral Coefficients Whose Zeros Include Pdf Free Download

The Random Variable X Has A Probability Distribution P X O

Solved Let X Be A Discrete Random Variable With The Follo Chegg Com

How To Find The Probability Using Discrete Variables Socratic

Solved Function F X P X X 4k X 0 3k X 1 2k X Chegg Com

Q3 Prove That P K 1 1 Kr If R 1 Let F 0 R Be A Twice Differentiable Function With F 39 39 X 0 For All X

If X 1 P Y 1 Q Z 1 R And Xyz 1 Then What Is The Value Of P Q R Quora

Pdf Common Distributions Discrete Distributions And Continuous Distributions
If X 1 P Y 1 Q Z 1 R And Xyz 1 Then What Is The Value Of P Q R Quora

Obfuscated Hello World Program
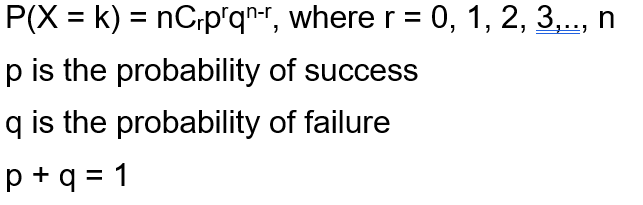
Binomial Distribution In R Programming Geeksforgeeks

1 Vytah

The Equilibrium Constant Kp For The Reaction Below Is 4 40 At 00 K 0 Calculate Ag For The R Homeworklib

Calculate The Mean For The Probability Distribution Find K And P X Is Greater Or Equal To 2 Youtube

Basic Probability Homework 2 Exercise 1 Where Does The

Introduction To Discrete Random Variables
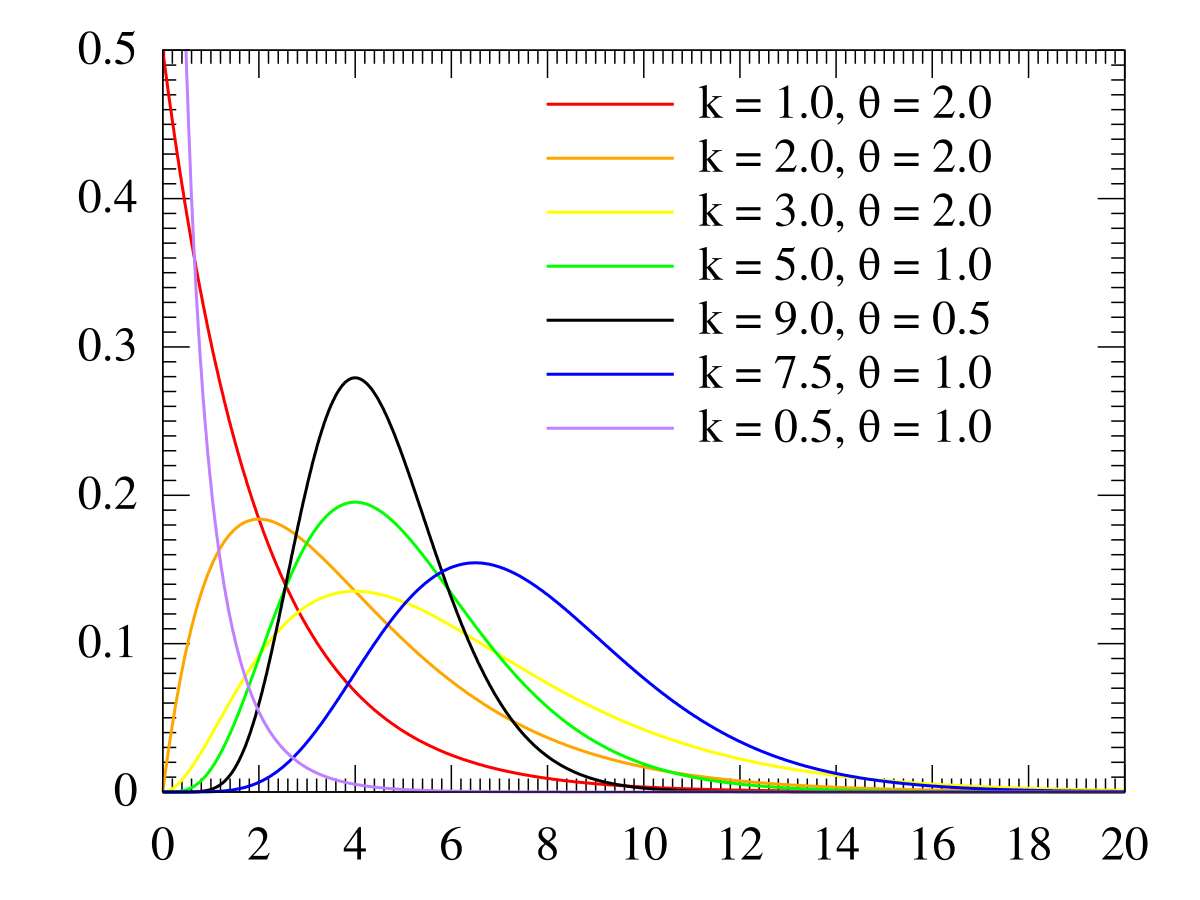
Gamma Distribution Wikipedia
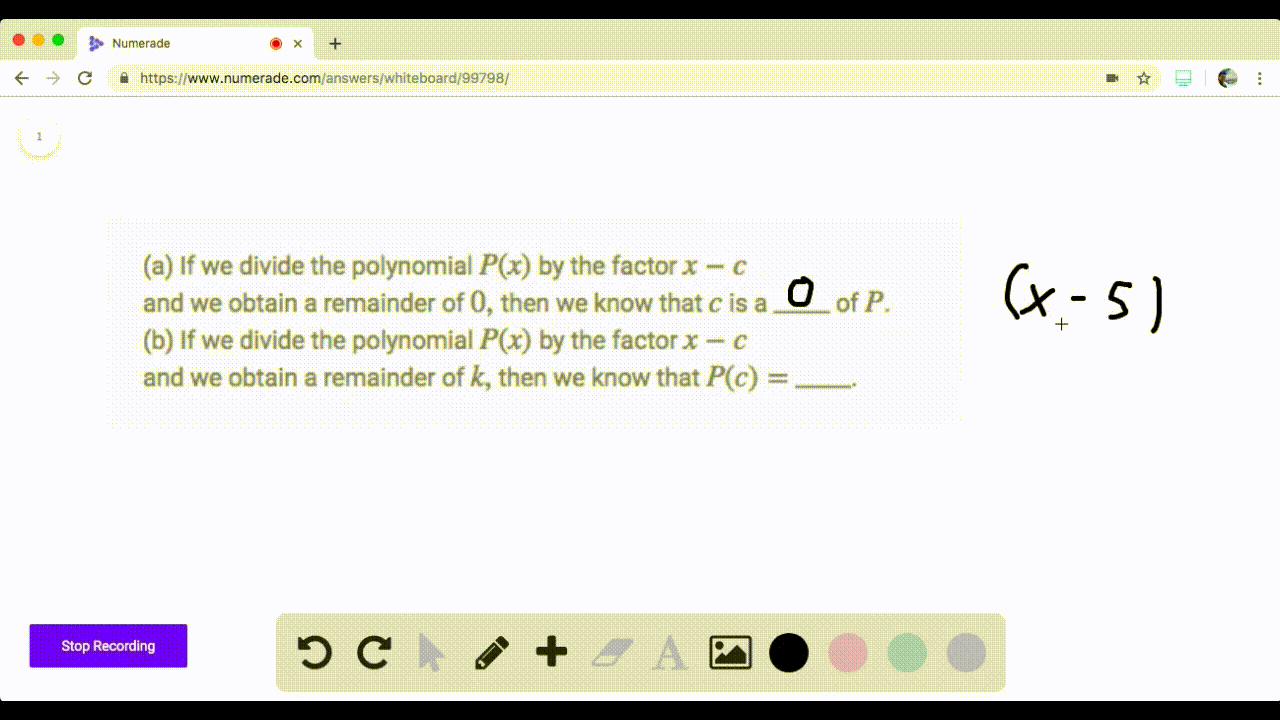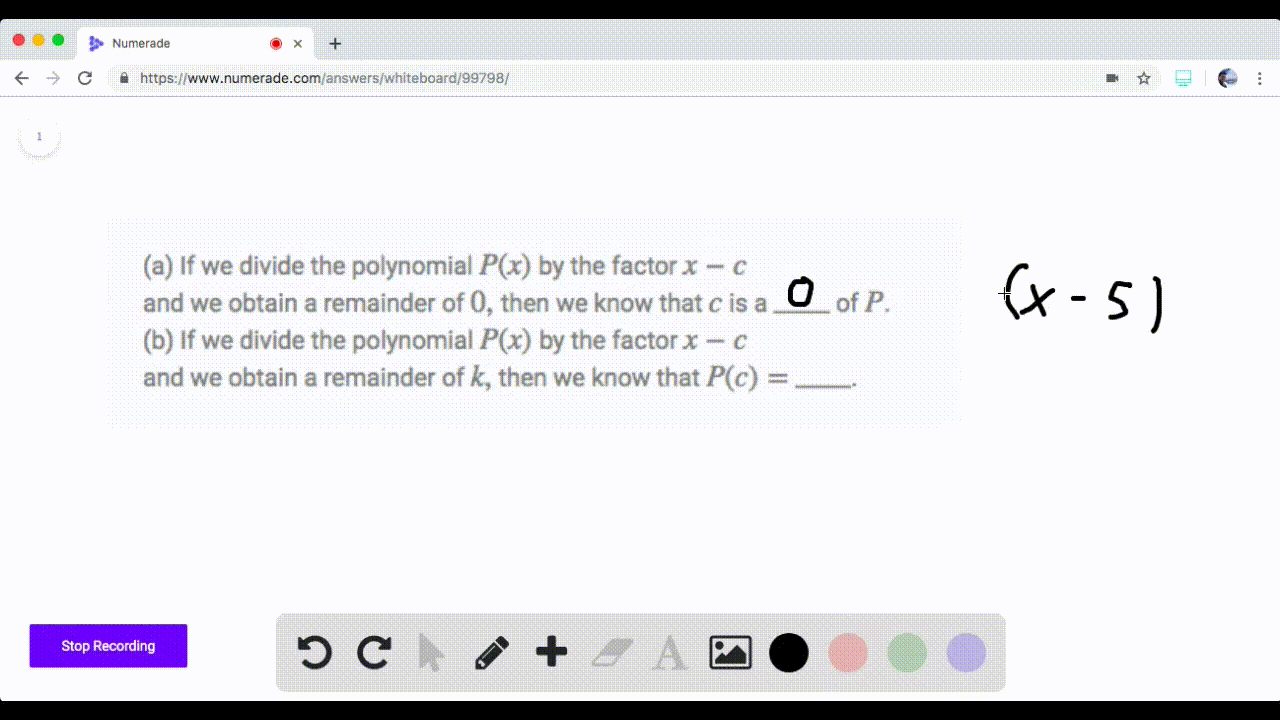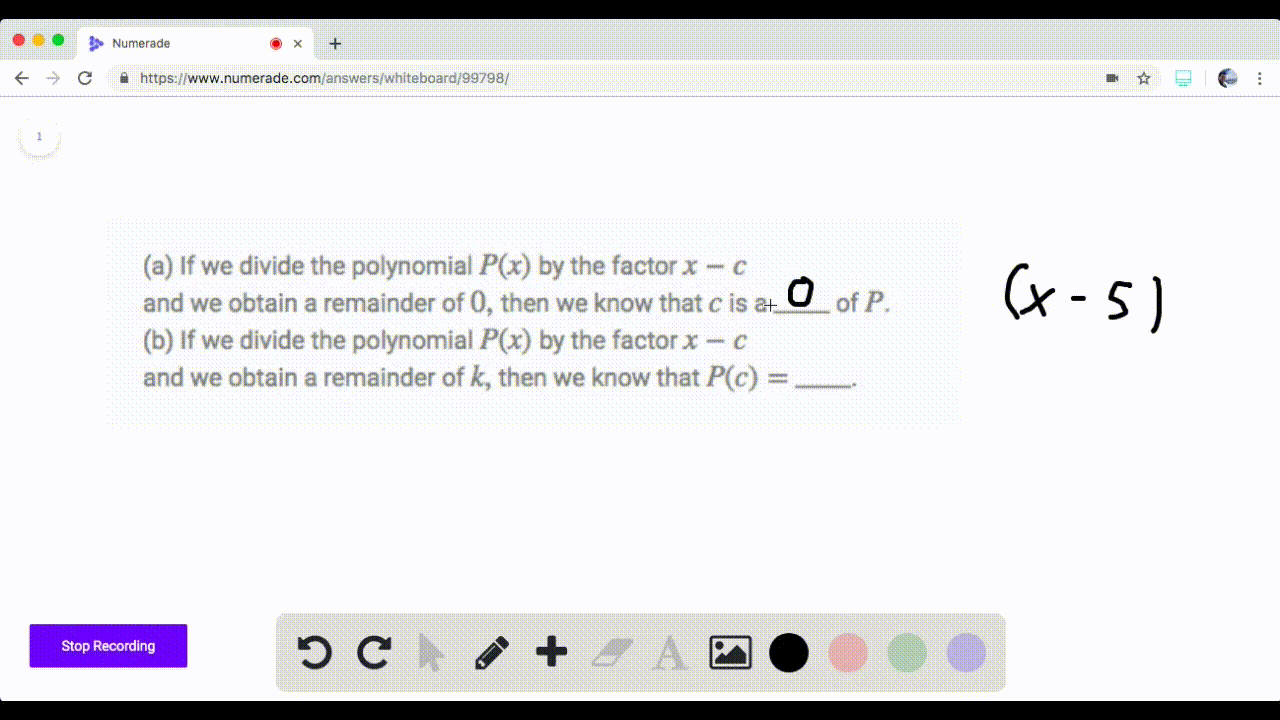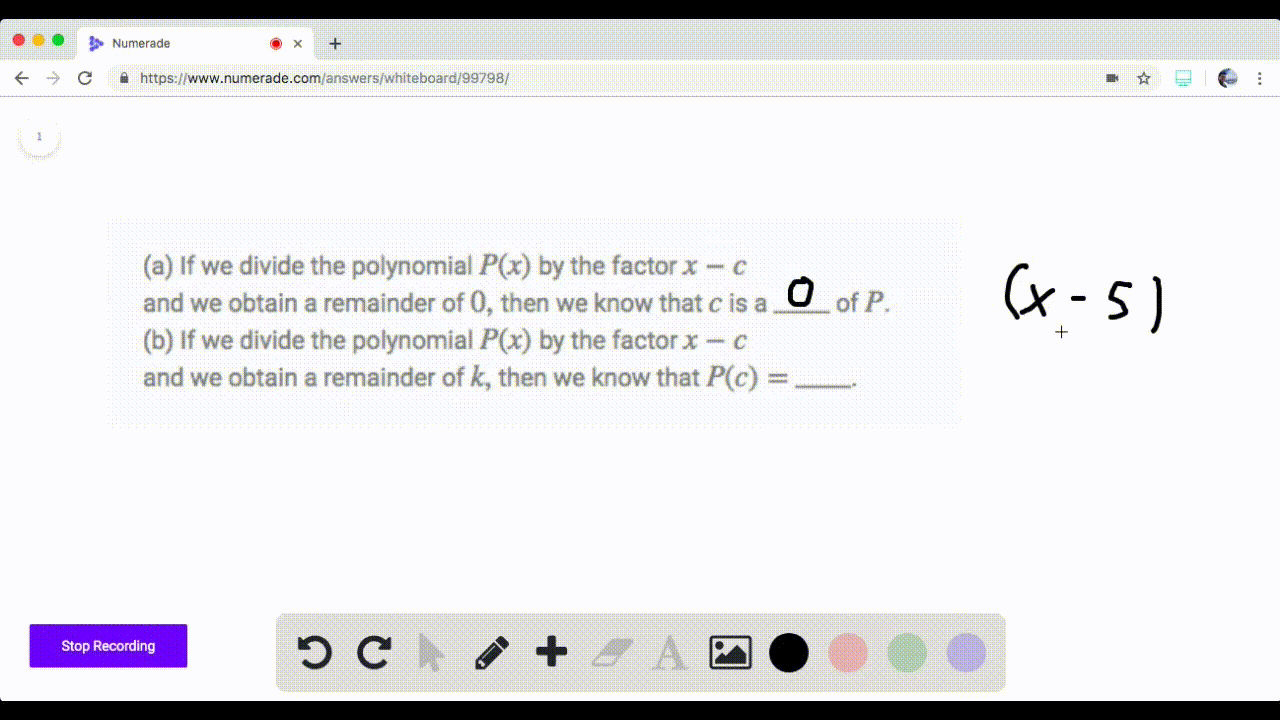
Solved If We Divide The Polynomial P By The Facto




